Rögtön meg is próbáltuk és elsőre igaznak bizonyult. Bár egy kis fejtörés után újra nekifutottunk és egy nagyobb újságpapírt sikerült hétszer összehajtanunk. Hogy mennyi a világrekord és mekkora lenne egy ötvenszer félbehajtott papírlap magassága? Kiderül.
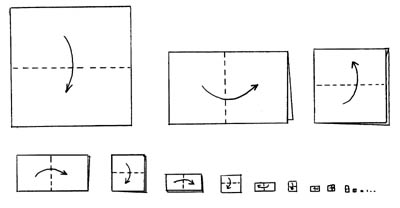
1 Hajtsuk félbe a papírt a vonal mentén.
2 Megint.
3 Megint.
4 Megint.
5 Megint.
6 Megint.
7 Megint.
8,9,10,11,12… stb. Megint megint.
Vajon meddig jutunk?
Mytbustersék ki is próbálták egy focipályányi papírlappal (meg egy kis úthengeres segítséget igénybe véve), és 11-ig jutottak.
hirdetés
A világrekord 2002 óta 12 félbehajtás, beállítója Britney Gallivan, akinek teljesítményéről illetve afélbehajtás problematikájáról, képletéről külön Wikipédia oldal emlékezik meg.
És hogy mi lenne, ha egy papírlapot ötvenszer félbe tudnánk hajtani? Malcolm Gladwell így ír erről Fordulópont című könyvében:
„Adjunk valakinek egy nagy ív papírt és azt kérjük, hajtsa össze egyszer, aztán fogja ezt az összehajtott papírt, és még egyszer hajtsa össze, aztán még egyszer és még egyszer, egészen addig amíg ötvenszer el nem végezte a hajtás műveletét. Aztán megkérdezzük, mit gondol, milyen magas lesz az összehajtogatott papír. A kérdésre a legtöbben úgy válaszolnak, hogy gondolatban összehajtják a papírt, és azt mondják, olyan vastag lenne, mint egy telefonkönyv, vagy ha elég merészek, azt mondják, olyan magas lenne, mint egy hűtőszekrény. Ám a valódi, a helyes válasz az, hogy körülbelül olyan magas lenne, mint a Föld-Nap távolság, és ha még egyszer összehajtanánk, kétszeres Föld-Nap távolságot kapnánk. Ez a példa a matematikában mértani sorozatként, avagy mértani haladványként ismeretes. … Az embernek elég nehéz ezt a fajta haladványt hétköznapi ésszel felfogni, mert az eredmény – a hatás – igen aránytalannak látszik a kiinduló ponthoz képest.”
Aki pedig ennél is többre vágyik, az itt látható táblázatban a 100. hajtogatás hatásáig is eljut. Aztán már nincs tovább, legalábbis ebben az univerzumban.
Egész konkrétan úgy lenne jó a kocsmai feladvány, ha meghatároznánk a papírlap méretét, mégpedig egy A4-es lapban.
Ugyanis az A4-es papírt ha nyolcszor összehajtod, már örülhetsz. De ennyi is elég kétséges lenne, maximum hidraulikus prés alatt.
hirdetés
Ahogy azt már említettük a papírlap félbehajtásának jelenlegi rekordja 12, annál többször még senki nem tudott egymásután félbehajtani egy lapot. Éppen ezért az alábbi gondolatkísérlet végig gondolatkísérlet marad, nem tudjuk gyakorlatba átemelni, de azért érdekes elgondolkozni a tudományrajongó Nikola Slavkovicáltal összegyűjtött, matematikailag igazolható érdekességeken.
A 80 g-os papír 0,1 mm-es. Ezt egyszer hajtva 0,1 * 2, kétszer hajtva 0,1mm * 2 * 2, ötször hajtva 0,1 * 52 mm, tízszer hajtva 0,1 * 102 mm lesz. Azaz kb. 10 cm-es "papírvastagság" lesz tökéletes hajtás esetén. Már csak az a kérdés, hogy ezt a vastagságot milyen technikával éred el. Mert nincs ilyen.
Azonban ha a kérdést úgy módosítjuk, hogy a papír mérete nem definiált, akkor egy standard (0,1 mm) vastagságú papír hány hajtás után érné el a Holdat, arra a válasz:
Ha a Föld-Hold távolságot 384.000 km-nek vesszük, akkor az képlet valahogy így nézne ki:
0,1*(-610) * X2 = 384.000
Kicsit átrendezve az egyenletet
X2=384.000/0,0000001, azaz
X2= 3.840.000.000.000
Ez pedig valahol az 41<x<42 esetén teljesül, vagyis a 41. összehajtásnál MÉG nem érjük el a Holdat, a 42. hajtásnál pedig MÁR túl is szárnyaltuk.
Tehát 0,1 mm-es vastagságú papír esetén 42 TÖKÉLETES hajtással érhetjük el a Holdat.
Tehát ha egy átlagos papírlap vastagsága 0,1 mm-es, akkor 23 egymásutáni félbehajtás után már több mint 1 km magas lenne a lapból formálódó oszlop. Ha azt szeretnénk, hogy az oszlop 100 km-es legyen, ahhoz 30 félbehajtásra van szükség. 42-ből már a Holdig is elérne a papír, 51 félbehajtás után pedig már a Napnál járna. Aki az ismert univerzum 93 milliárd fényéves átmérőjét szeretné egy papírral elérni, annak nem lenne más dolga, mint 103 alkalommal félbehajtani a lapot.
Hogy mindez miért hangzik annyira hihetetlennek? Az agyunk lineárisan gondolkodik, az exponenciálisan változó trendekkel egyszerűen nem tud mit kezdeni.
Próbáld ki Te is egy papírlappal! Egy fogadás tárgyának jól jöhet.
hirdetés








 Megosztás
Megosztás